
About
License
Download
Publications
Examples
Links
Thanks
The aaflib is an implementation of the mathematical construct of affine arithmetics in C++. This construct has been introduced by Stolfi et. al. Their c-library can be found at http://www.ic.unicamp.br/~stolfi/EXPORT/software/c/Index.html#libaa. The aaflib is based on the libaffa, a reimplemention of the original library, but has been developed further. It has been used as main calculation library for a spice-like nonlinear circuit simulator. Currently the library and the simulator are developed at the Institute of Microelectronic Systems in Hannover, Germany.
This project is only distributed as source. The packaged sources can be found under:
http://sourceforge.net/projects/aaflib/files/
If you want to participate in this project or want the most current version you can also use the svn-repository with:
svn co http://svn.code.sf.net/p/aaflib/code/ aaflib-code
This program is free software;
you can redistribute it and/or modify it under the terms of the GNU Lesser General Public License as published by the Free Software Foundation;
either version 2.1 of the License, or (at your option) any later version.
This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY;
without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.
See the GNU Lesser General Public License for more details.
A copy of the GNU Lesser General Public License can be found at http://www.gnu.org/licenses/old-licenses/lgpl-2.1.html
If you are using this enhanced version or any part of it, in or for your publications or applications, please consider citing at least one of the mentioned Publications.
All references are also available for download as bibtex-file.
| Author | Title | Year | Journal/Proceedings | Reftype |
|---|---|---|---|---|
| Barke, M., Kargel, M., Lu, W., Salfelder, F., Hedrich, L., Olbrich, M., Radetzki, M. and Schlichtmann, U. | Robustness validation of integrated circuits and systems | 2012 | 2012 4th Asia Symposium on Quality Electronic Design (ASQED), pp. 145-154 | inproceedings |
| Freisfeld, M. | Semi-symbolische Modellierung und Simulation von Unsicherheiten in analogen Schaltungen mit Hilfe stückweise affiner Abbildungen | 2009 | School: Institut für Mikroelektronische Systeme | phdthesis |
| Freisfeld, M., M.Olbrich, Grimm, C. and Barke, E. | Verwendung von Gebietsarithmetiken zum Entwurf robuster Schaltungen und Systeme | 2007 | 1.GMM/GI/GI-Fachtagung Zuverlaessigkeit und Entwurf, pp. 131-136 | inproceedings |
| Freisfeld, M., Olbrich, M. and Barke, E. | Circuit Simulations with Uncertainties using Affine Arithmetic and Piecewise Affine Statemodels | 2008 | Proceedings of International Conference on Solid-State and Integrated-Circuit Technology | inproceedings |
| Freisfeld, M., Olbrich, M., Pfost, M. and Barke, E. | Verlässliche Modellierung integrierter analoger Schaltungen durch stückweise affine Abbildungen | 2008 | (56)10. GMM/ITG-Fachtagung Analog 2008 | inproceedings |
| Grabowski, D. | Gebietsarithmetische Verfahren zur Simulation analoger Schaltungen mit Parameterunsicherheiten | 2009 | School: Institut für Mikroelektronische Systeme | phdthesis |
| Grabowski, D., Grimm, C. and Barke, E. | Ein Verfahren zur effizienten Analyse von Schaltungen mit Parametervarianzen | 2006 | 9. Workshop: Methoden und Beschreibungssprachen zur Modellierung und Verifikation von Schaltungen und Systemen (MBMV), pp. 181-190 | inproceedings |
| Grabowski, D., Grimm, C. and Barke, E. | Semi-Symbolic Modeling and Simulation of Circuits and Systems | 2006 | IEEE International Symposium on Circuits and Systems (ISCAS 2006), pp. CD-ROM | inproceedings |
| Grabowski, D., Olbrich, M. and Barke, E. | Simulation analoger Schaltungen mit affiner Arithmetik | 2008 | Vol. 2. GMM/GI/ITG-Fachtagung "Zuverlässigkeit und Entwurf"2. GMM/GI/ITG-Fachtagung uverlässigkeit und Entwurf |
inproceedings |
| Grabowski, D., Olbrich, M. and Barke, E. | AC-Analyse analoger Schaltungen mit affiner Arithmetik | 2008 | Vol. Entwicklung von Analogschaltungen mit CAE-MethodenAnalog 2008, pp. 63-68 |
inproceedings |
| Grabowski, D., Olbrich, M. and Barke, E. | Analog Circuit Simulation Using Range Arithmetics | 2008 | Vol. Proceedings of the ASP-DAC 2008ASP DAC 2008, pp. 762-767 |
inproceedings |
| Grabowski, D., Olbrich, M., Grimm, C. and Barke, E. | Range Arithmetics to Speed up Reachability Analysis of Analog Systems | 2007 | FDL 2007, pp. CD-ROM | inproceedings |
| Heupke, W., Grimm, C. and Waldschmidt, K. | Modeling Uncertainty in Nonlinear Analog Systems with Affine Arithmetic | 2006 | Applications of Specification and Design Languages for SoCs, pp. 155-169 | incollection |
| Heupke, W., Grimm, C. and Waldschmidt, K. | Semi-Symbolic Simulation of Nonlinear Systems | 2005 | Forum on Specification and Design Languages (FDL'05), Lausanne, September 2005, pp. CD-ROM | inproceedings |
| Kaergel, M., Schupfer, F., Grimm, C., Olbrich, M. and Barke, E. | Towards abstract analysis techniques for range based system simulations | 2010 | Specification Design Languages (FDL 2010), 2010 Forum on, pp. 1-6 | inproceedings |
| Krause, A., Olbrich, M. and Barke, E. | Enclosing the modeling error in analog behavioral models using neural networks and affine arithmetic | 2012 | 2012 International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Applications to Circuit Design (SMACD), pp. 5-8 | inproceedings |
| Scharf, O., Olbrich, M. and Barke, E. | Lösungsverfahren für nichtlineare implizite Gleichungssysteme unter Verwendung von Affiner Arithmetik und Gebietsaufteilungen | 2013 | GMM Fachbericht Analog 2013 | conference |
| Scharf, O., Olbrich, M. and Barke, E. | Anwendung der affinen Arithmetik auf das BSIMSOI-Modell zur Simulation von Parameterschwankungen | 2011 | GMM Fachbericht Analog 2011 | conference |
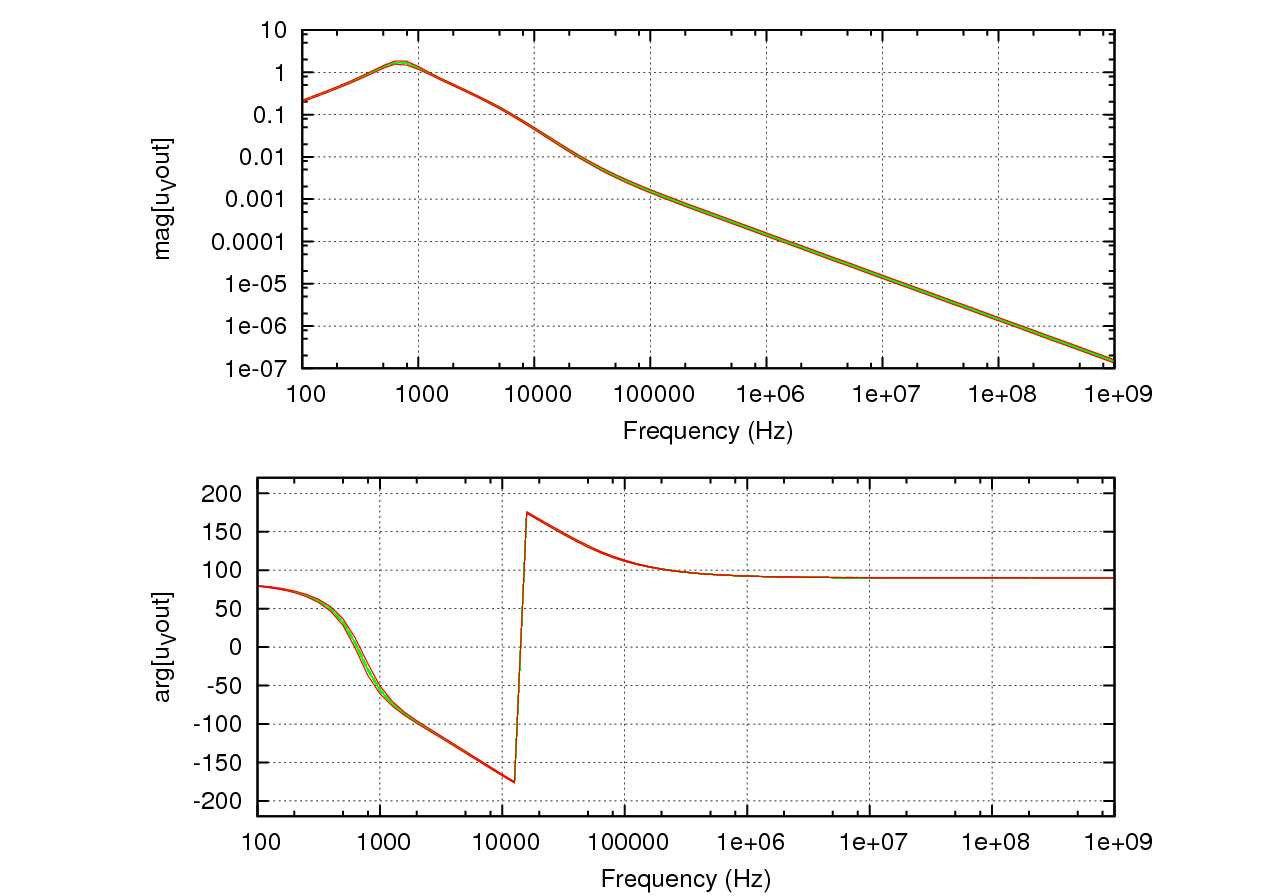
In this section, we show some example plots of the affine simulator.
The affine arithmetic has been used, to allow simulation of parameter variations in one simulation run.
Each uncorrelated parameter variation has been assigned a unique deviation symbol.
In the results you can see in red the borders of the affine simulation, in green are regular simulations using Monte-Carlo-Samples for the variations.
A transient simulation of a bandpass.

A AC simulation of the same circuit.
http://www.ic.unicamp.br/~stolfi/EXPORT/software/c/Index.html#libaa
http://www.nongnu.org/libaffa
http://en.wikipedia.org/wiki/Affine_arithmetic
http://www.ims.uni-hannover.de
Thanks to the German BMBF for financing the work on this library.